Kwantyle w szeregu szczegółowym
Wprowadzenie
Jednym z zagadnień statystyki opisowej, gdzie wśród autorów podręczników i nauczycieli akademickich nie ma konsensusu, jest kwestia obliczania kwantyli (w szczególności kwartyli, mediany) dla danych podanych w postaci szeregu szczegółowego (indywidualnego). Kwantyle stanowią jedno z kluczowych pojęć w statystyce opisowej. W tym artykule przyjrzymy się, czym kwantyle w statystyce są naprawdę, jak definiuje się je w szeregu szczegółowym oraz dlaczego sposób ich przedstawiania w podręcznikach akademickich często budzi wątpliwości.
O ile dla szeregów rozdzielczych przedziałowych w zasadzie obowiązuje jednolity wzór:
$$q = {x_{0m}} + {{{N_q - nsk_{m-1}} \over n_m} \cdot h_m}$$
gdzie:
- $x_{0m}$ jest lewym krańcem przedziału zawierającego dany kwantyl,
- $N_q = n \cdot q$ jest numerem pozycji danego kwantyla,
- $nsk_{m-1}$ jest skumulowaną liczebnością przedziału poprzedzającego przedział zawierający kwantyl; jeśli kwantyl jest w przedziale pierwszym, przyjmuje się $nsk_0 = 0$,
- $n_m$ jest liczebnością przedziału zawierającego kwantyl,
- $h_m$ jest długością przedziału zawierającego dany kwantyl.
Użycie tego wzoru wymaga ustalenia, w którym przedziale znajduje się kwantyl – jest to najniższy przedział, którego liczebność skumulowana jest równa co najmniej $N_q$.
o tyle w przypadku szeregów szczegółowych podejścia są bardzo różne.
Najczęściej stosowane wzory na kwantyle
Pełna zgodność panuje w zasadzie tylko przy obliczaniu mediany. Obowiązuje tutaj zasada, że medianę oblicza się w zależności od tego, czy liczebność zbioru danych jest parzysta, czy nieparzysta.
Dla parzystej ilości danych, medianę oblicza się jako średnia arytmetyczną dwu „środkowych” elementów uporządkowanego ciągu danych, tj:
$$Me={{x_{n \over 2} + x_{{n \over 2} +1}} \over 2}$$
dla szeregu zawierającego nieparzystą ilość danych, mediana równa jest wartości „środkowej”, tj.:
$$Me=x_{{n+1} \over 2}$$
jeśli jednak chodzi o pozostałe kwartyle, czy też kwantyle innych rzędów (np. decyle, centyle) jednolitości takiej już nie ma.
Kwartyle – dolny ($Q_1$) oraz górny ($Q_3$) obliczane są – według nauczycieli akademickich na większości polskich uczelni – na jeden z dwu sposobów:
- według sposobu podanego w „kultowym” podręczniku W. Krysicki, J. Bartos, K. Królikowska i inni Rachunek prawdopodobieństwa i statystyka matematyczna w zadaniach, tj. szereg danych dzielony jest na dwie grupy – do pierwszej zalicza się wszystkie wartości mniejsze od mediany i medianę, a do drugiej medianę i wszystkie wartości większe od mediany – i następnie kwartyl dolny oblicza się, jako medianę pierwszej, a górny – jako medianę drugiej grupy wartości.
- poprzez „zaokrąglenie” (zazwyczaj za pomocą funkcji entier – zwanej swojsko „podłogą”) wartości $n \over 4$ oraz ${3 \over 4} n$ i przyjęcie wartości kwartyla równej wartości w uporządkowanym szeregu danych, stojącej na tak obliczonych pozycjach. Co gorsze, niektórzy nauczyciele akademiccy zamiast $n$ stosują $n+1$… Ręce opadają.
O ile pierwszy z wymienionych sposobów można uznać za w miarę logiczny i zasadny, choć niepozbawiony kontrowersji zwłaszcza w sytuacji, gdy kilka wartości w szeregu równych jest medianie (przy literalnym traktowaniu podręcznikowego przepisu należałoby wartość taką wziąć tylko raz), o tyle drugi ze sposobów nie może być nazwany inaczej, jak „radosna twórczość” akademickich nauczycieli całkowicie pozbawionych statystycznego „wyczucia”.
Największy mankament pierwszego z opisywanych sposobów jest taki, że za pomocą tego schematu obliczyć można w zasadzie tylko kwartyle. Przeprowadzając dalsze „połowienie” szeregu danych, w analogiczny sposób można policzyć np. kwantyle rzędu 0,125; 0,375,… (oktyle?), ale nie znajdują one zastosowania w praktyce statystycznej.
Drugi z opisywanych sposobów jest całkowicie bezsensowny chociażby przez to, że „na siłę” dopasowuje kwartyle, czy też wyliczane kwantyle innych rzędów, dokładnie do wartości danych z szeregu, podczas gdy przykład mediany dla parzystej ilości danych pokazuje, że nie zawsze wartość kwantyla musi rekrutować się spośród wartości z szeregu. Taka zbieżność wręcz, o ile nie mówimy o szeregu rozdzielczym punktowym, gdzie sporo wartości się powtarza, jest na ogół wyłącznie dziełem przypadku (czy raczej występuje wyłącznie dla konkretnych wartości $n$ – i w przypadku kwartyli bynajmniej nie są to wartości podzielne przez 4, co dobitnie pokazuje mediana, która wprost równa jest wartości z szeregu tylko dla nieparzystych (a zatem niepodzielnych przez 2) wartości.
Najgorsze i najbardziej groteskowe w tym wszystkim jest to, że jako korepetytor przygotowujący studentów do kolokwiów i egzaminów, sam muszę ich tych sposobów uczyć… Czuję się wówczas, jak katecheta, który wziął zastępstwo za polonistkę i przerabia akurat mitologię grecką.
Okazuje się, że pojęcie o obliczaniu kwantyli w szeregu szczegółowym mają jedynie programiści firmy Microsoft…
Jak powinniśmy obliczać kwantyle w szeregu szczegółowym?
Jak wiemy, „idealne” do obliczenia mediany są szeregi szczegółowe o nieparzystej ilości danych. Dla przypomnienia, weźmy szereg o pięciu elementach. Jako, że tym etapie interesuje nas wyłącznie pozycja elementu, a nie jego wartość, toteż zamiast liczb rozważać będziemy „kółka”. Każdorazowo pisząc o szeregu, będziemy mieli na myśli uporządkowany ciąg danych od najmniejszej do największej wartości.

Położenie mediany w szeregu szczegółowym o pięciu elementach
Jak widać, medianą jest trzeci element, gdyż zgodnie z „filozofią” mediany, tyle samo elementów jest na lewo od niego, ile elementów jest po jego prawej stronie.
Pozycję mediany wyznaczyć tutaj możemy, jako: $N_{Me} = {{n + 1} \over 2}$
W tym samym szeregu zauważymy również, że idealnymi kwartylami: dolnym i górnym są odpowiednio drugi oraz czwarty element:


Położenie kwartyli (dolnego i górnego) w szeregu szczegółowym o pięciu elementach
Dlaczego tak? A dlatego, że pierwszy element po swojej prawej stronie ma dokładnie trzy razy więcej elementów niż po swojej lewej stronie (1 vs 3 tak samo, jak 25% vs 75%) i analogicznie czwarty element ma po swojej lewej stronie trzykrotnie więcej elementów, niż po prawej.
Jak się za chwilę okaże, takie „dokładne trafienie” w pozycję kwartyla ma miejsce zawsze, gdy ilość elementów szeregu jest postaci $4k+1$, czyli przy dzieleniu przez cztery daje resztę jeden.
Który jednak element, jako kwartyl, wskażą wspomniane wcześniej dwa najpopularniejsze w nauczaniu akademickim sposoby? W przypadku sposobu z podręcznika „Krysicki i inni”, wszystko zależy od konkretnych wartości. Dla szeregu bowiem:
1; 2; 3; 4; 5
Medianą jest 3 i obie grupy mieć będą postaci: 1; 2; 3 oraz 3; 4; 5 i jako kwartyle dolny i górny poprawnie wskazane zostaną liczby odpowiednio 2 oraz 4. Jednak już dla szeregu:
1; 2; 2; 3; 3
Medianą jest 2 i pierwszą grupę (elementy mniejsze od mediany i medianę) tworzą liczby 1, 2 a ich medianą, czyli pierwszym kwartylem jest liczba 1,5.
Drugi ze sposobów daje jeszcze dziwniejsze wyniki. $n=5$, zatem $Q_1 = x_{\left[ n \over 4 \right]} = x_{[1,25]}=x_1$ oraz $Q_3 = x_{\left[ {3 \over 4} \cdot n \right]} = x_{[3,75]}=x_3$ Przyjmując zasadę zaokrąglania matematycznego, zamiast funkcji „podłoga” otrzymamy w tym akurat wypadku prawidłowy wynik $Q_3=x_4$.
Nieco lepiej sprawa będzie wyglądać, gdy – jak to niektórzy nauczyciele akademiccy robią – zamiast $n$ użyjemy $n+1$. Zaokrąglając za pomocą funkcji „podłoga” otrzymamy $Q_1=x_1$ oraz $Q_3=x_4$ natomiast zaokrąglając matematycznie uzyskamy $Q_1=x_2$ oraz $Q_3=x_5$ (sic!).
Oczywiście zupełnie bezsensowne rezultaty tą metodą otrzymamy dla ilości elementów niespełniających warunku $n = 4k +1$. Wówczas bowiem, jako kwartyle zostają cały czas wskazane konkretne elementy z szeregu, podczas gdy intuicja powinna nam mówić, że muszą to być jakieś elementy „pośrednie” – tak, jak dzieje się to w przypadku mediany przy parzystej ilości elementów.
Jak zatem podejść do problemu?
Otóż, aby wyznaczyć kwartyle i dowolnego rzędu inne kwantyle w szeregu szczegółowym, należy zacząć od wyznaczenia w prawidłowy sposób, pozycji tego kwantyla. Jeśli będzie to liczba całkowita, wówczas kwantylem będzie wartość w szeregu stojąca na tej właśnie pozycji. Jeśli będzie to pozycja o wartości ułamkowej, kwantyl otrzymamy interpolując liniowo wartość stojącą na pozycji równej wyznaczonej pozycji kwantyla zaokrąglonej w dół i kolejnej wartości.
Rozważmy szereg zawierający $n$ elementów. Zgodnie z najczęściej stosowanym w statystyce zwyczajem, elementy te numerujemy indeksami od $1$ do $n$. Stąd wynika, że długość takiego szeregu wynosi $n-1$. Zrozumienie tego, prostego skądinąd, faktu jest kluczowe dla prawidłowego liczenia kwantyli w szeregu szczegółowym.

„Odległość” pomiędzy danymi w szeregu szczegółowym
W takiej sytuacji, przykładowo mediana znajdować się powinna w „odległości” ${n-1} \over 2$ od pierwszej wartości szeregu, kwartyl dolny w odległości ${n-1} \over 4$ i – ogólnie – kwantyl rzędu $q$ w odległości $(n-1) \cdot q$.
Zaraz zaraz, czy aby na pewno $n - 1$? Na pewno! Zauważmy, że wprawdzie odległość liczymy od zera, ale dane indeksujemy od 1, stąd aby wyliczyć pozycję kwantyla, należy do tak wyliczonej odległości dodać 1.
Wówczas pozycja mediany wynosi:
$$N_{Me} = {{n-1} \over 2} + 1 = {{n-1+2} \over 2} = {{n+1} \over 2}$$
Eureka! Już wiemy, skąd we wzorze wzięło się $n+1$, w bezrefleksyjny sposób przenoszone przez wielu prowadzących zajęcia ze statystyki na wyższych uczelniach, na kwantyle innego rzędu.
W przypadku bowiem kwantyli innego rzędu, $n+1$ już się nie pojawi, gdyż wzór na numer pozycji będzie miał postać:
$$N_q = {{\left( n - 1 \right) q} + 1}$$
Jeśli tak wyliczony numer pozycji okaże się liczbą całkowitą, to – jak wspomniano wyżej – kwantyl równy będzie po prostu wskazanemu elementowi. Co jednak, jeśli pozycja kwantyla wyjdzie wartością ułamkową?
Wyprowadzamy prawidłowy wzór na kwantyl rzędu q
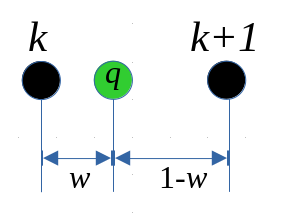
Kwantyl o pozycji niebędącej liczbą całkowitą
Załóżmy, że pozycja kwantyla $q$ wynosi $k+w$, gdzie k jest częścią całkowitą $k=\left[ N_q \right]$ natomiast $w$ jest częścią ułamkową. W takiej sytuacji logicznym jest, że kwantyl $q$ powinien zostać wyznaczony poprzez interpolację liniową wartości $x_k$ oraz $x_{k+1}$.
Dokonajmy takiej interpolacji:
$$q=x_k + \left(x_{k+1} - x_k \right) \cdot w = x_k \cdot \left(1 - w \right) + x_{k+1} \cdot w$$
Jak widać, kwantyl $q$ jest średnią ważoną wartości na pozycjach $k$ oraz $k+1$ w szeregu, gdzie wagami przy wartości na danej pozycji szeregu są odległości od drugiej z pozycji.
W takiej sytuacji, wzór na kwantyl rzędu $q$ może być zapisany w następującej postaci:
$$q = {x_{\left[ (n-1) \cdot q +1 \right]} \cdot \left( \left[(n-1) \cdot q \right] + 1 - (n-1) \cdot q \right) + x_{\left[ (n-1) \cdot q +1 \right]+1} \cdot \left( (n-1) \cdot q - \left[(n-1) \cdot q \right] \right) } $$
lub nieco prościej, wykorzystując wynikający z monotoniczności dodawania fakt, że $x - a - \left[x -a \right] = x - \left[ x \right]$:
$$q = {x_{\left[ (n-1) \cdot q +1 \right]} \cdot \left( \left[n \cdot q \right] + 1 - n \cdot q \right) + x_{\left[ (n-1) \cdot q +1 \right]+1} \cdot \left( n \cdot q - \left[n \cdot q \right] \right) } $$
gdzie oczywiście $\left[ x \right]$ jest funkcją „podłoga”, znaną także pod nazwą funkcji entier, czyli największa liczbą całkowita nie większa od $x$ (kiedyś, w czasach popularności tablic logarytmicznych, funkcja ta nazywała się po prostu cechą liczby $x$).
Wyprowadzony wzór wygląda dość skomplikowanie. Można go jednak zapisać w postaci prostego algorytmu.
- Wyznacz numer pozycji kwantyla $N_q = {\left(n - 1 \right) \cdot q} + 1$
- Jeśli tak wyznaczony numer jest liczbą całkowitą, to $q={x_{N_q}}$, czyli szukany kwantyl jest równy elementowi uporządkowanego szeregu na wyznaczonej pozycji. Kończymy obliczenia. W przeciwnym razie wykonaj punkt 3.
- Niech $k=\left[ N_q \right]$, tj. zaokrąglamy w dół wartość $N_q$ i wyznaczamy w ten sposób k-tą pozycję w szeregu. Jeśli $x_k = x_{k+1}$, tj. jeśli wartości w szeregu na pozycjach $k$ oraz $k+1$ są jednakowe, to ich wspólna wartość jest obliczaną wartością kwantyla: $q = x_k = x_{k+1}$. Kończymy obliczenia. W przeciwnym razie przechodzimy do pkt 4.
- Niech $w$ oznacza część ułamkową wyznaczonej pozycji kwantyla: $w=N_q - \left[ N_q \right]$. Obliczamy wartość kwantyla, jako: $q = x_k \cdot (1-w) + x_{k+1} \cdot w$.
Ten sposób oczywiście działa również dla mediany, dając identyczne wyniki z „klasycznym” sposobem, albowiem dla parzystej wartości $n$, numer pozycji $N_{Me} = \left( n - 1 \right) \cdot 0.5 +1 = {{n+1} \over 2} $ posiada część ułamkową $w=0,5$ i medianą jest średnią ważoną z liczb na pozycjach $n \over 2$ oraz ${n \over 2} + 1$ z obiema wagami równymi 0,5, a zatem ich średnią arytmetyczną.
Przykłady
Przykład nr 1
Weźmy uporządkowany szereg o 11 elementach: 2; 3; 5; 5; 7; 9; 10; 18; 21; 24; 25
Obliczmy dla tego szeregu najczęściej liczone kwantyle, tj.: medianę, dolny (pierwszy) oraz górny (trzeci) kwartyl, używane do wyliczenia pozycyjnych wersji odchylenia ćwiartkowego, współczynnika zmienności oraz współczynnika asymetrii a także decyle pierwszy oraz dziewiąty, służące do wyliczenia pozycyjnego współczynnika skupienia.
Pozycje poszczególnych kwantyli wynoszą:
- decyl pierwszy: $N_{d_1}=(11-1) \cdot 0,1 +1 = 10 \cdot 0,1 + 1 = 1+1=2$
- kwartyl pierwszy: $N_{Q_1}=(11-1) \cdot 0,25 +1 = 10 \cdot 0,25 + 1 = 2,5+1=3,5$
- mediana: $N_{Me}=(11-1) \cdot 0,5 +1 = 10 \cdot 0,5 + 1 = 5+1=6$
- kwartyl trzeci: $N_{Q_3}=(11-1) \cdot 0,75 +1 = 10 \cdot 0,75 + 1 = 7,5+1=8,5$
- decyl dziewiąty: $N_{d_9}=(11-1) \cdot 0,9 +1 = 10 \cdot 0,9 + 1 = 9+1=10$
Jak widać, oba decyle i mediana mają całkowite numery pozycji, zatem są one równe wprost odpowiednim elementom szeregu:
$d_1 = x_2 = 3$
$Me = x_6 = 9$
$d_9 = x_{10} = 24$
Natomiast części ułamkowe numerów kwartyli równe są 0,5 co oznacza, że są one równe de facto średnim arytmetycznym dwu sąsiednich elementów: kwartyl pierwszy jest średnią elementów trzeciego oraz czwartego natomiast kwartyl trzeci – ósmego i dziewiątego.
$Q_1 = x_3 \cdot 0,5 + x_4 \cdot 0,5 = 5 \cdot 0,5 + 5 \cdot 0,5 = 5$
Tutaj oczywiście oba elementy były równe, więc można było od razu wykorzystać pkt. trzeci przytoczonego wyżej algorytmu.
$Q_3= x_8 \cdot 0,5 + x_9 \cdot 0,5 = 18 \cdot 0,5 + 21 \cdot 0,5 = 19,5$
Kwartyl trzeci jest zatem interpolowaną wartością spoza szeregu danych.
Przykład 2
Weźmy teraz szereg składający się z dziesięciu wartości: 3; 6; 10; 15; 15; 19; 21; 28; 35; 40.
Wyliczamy te same kwantyle.
Pozycje poszczególnych kwantyli wynoszą:
- decyl pierwszy: $N_{d_1}=(10-1) \cdot 0,1 +1 = 9 \cdot 0,1 + 1 = 0,9+1=1,9$
- kwartyl pierwszy: $N_{Q_1}=(10-1) \cdot 0,25 +1 = 9 \cdot 0,25 + 1 = 2,25+1=3,25$
- mediana: $N_{Me}=(10-1) \cdot 0,5 +1 = 9 \cdot 0,5 + 1 = 4,5+1=5,5$
- kwartyl trzeci: $N_{Q_3}=(10-1) \cdot 0,75 +1 = 9 \cdot 0,75 + 1 = 6,75+1=7,75$
- decyl dziewiąty: $N_{d_9}=(10-1) \cdot 0,9 +1 = 9 \cdot 0,9 + 1 = 8,1+1=9,1$
Tym razem wszystkie pozycje są ułamkowe. Wartości poszczególnych kwantyli obliczamy jako średnie ważone wartości na obu pozycjach „pomiędzy” którymi wypada wyliczona pozycja ułamkowa, tj. wartością zaokrągloną w dół i wartością następną.
Dla decyla pierwszego będzie to średnia ważona elementów na pozycjach 1 oraz 2. Ponieważ część ułamkowa wynosi 0,9, toteż wartość z pozycji pierwszej będzie ważona wartością 0,1 a wartość z pozycji drugiej – wagą 0,9.
$d_1 = x_1 \cdot 0,1 + x_2 \cdot 0,9 = 3 \cdot 0,1 + 6 \cdot 0,9 = 0,3 + 5,4 = 5,7$
W analogiczny sposób obliczamy pozostałe kwantyle:
$Q_1 = x_3 \cdot 0,75 + x_4 \cdot 0,25 = 10 \cdot 0,75 + 15 \cdot 0,25 = 7,5 + 3,75 = 11,25$
$Me = x_5 \cdot 0,5 + x_6 \cdot 0,5 = 15 \cdot 0,5 + 19 \cdot 0,5 = 7,5 + 6,5 = 17$
$Q_3 = x_7 \cdot 0,25 + x_8 \cdot 0,75 = 21 \cdot 0,25 + 28 \cdot 0,75 = 5,25 + 21 = 26,25$
$d_9 = x_9 \cdot 0,9 + x_10 \cdot 0,1 = 35 \cdot 0,9 + 40 \cdot 0,1 = 31,5 + 4 = 35,5$
Przykład 3
Weźmy dane w postaci szeregu rozdzielczego punktowego. Szereg rozdzielczy punktowy stanowi tak naprawdę efekt „kompresji bezstratnej” szeregu szczegółowego, zatem obowiązują dokładnie te same reguły. Ponieważ jednak znacznie częściej będzie się zdarzać, że dane się będą powtarzać, toteż obliczanie zazwyczaj będzie uproszczone (średnia ważoną dwu takich samych liczb równa jest tym liczbom, niezależnie od wag – punkt 3 algorytmu).
Do ustalenia pozycji poszczególnych elementów w szeregu, wykorzystujemy liczebności skumulowane. Wyliczamy ten sam zestaw kwantyli, co poprzednio.
| $x_i$ | $n_i$ | $nsk_i$ |
| 0 | 5 | 5 |
| 1 | 12 | 17 |
| 2 | 16 | 33 |
| 3 | 12 | 45 |
| 4 | 9 | 54 |
| 5 | 6 | 60 |
$n=60$
Obliczamy pozycje kwantyli:
Pozycje poszczególnych kwantyli wynoszą:
- decyl pierwszy: $N_{d_1}=(60-1) \cdot 0,1 +1 = 59 \cdot 0,1 + 1 = 5,9+1 = 6,9$
- kwartyl pierwszy: $N_{Q_1}=(60-1) \cdot 0,25 +1 = 59 \cdot 0,25 + 1 = 14,75 + 1= 15,75$
- mediana: $N_{Me}=(60-1) \cdot 0,5 +1 = 59 \cdot 0,5 + 1 = 29,5 + 1 = 30,5$
- kwartyl trzeci: $N_{Q_3}=(60-1) \cdot 0,75 +1 = 59 \cdot 0,75 + 1 = 44,25 + 1 = 45,25$
- decyl dziewiąty: $N_{d_9}=(60-1) \cdot 0,9 +1 = 59 \cdot 0,9 + 1 = 53,1+1 = 54,1$
W przypadku decyla pierwszego, zarówno na pozycji szóstej, jak i siódmej jest liczba 1, a zatem:
$d_1 = x_6 = x_7 = 1$
Analogicznie obliczając kwartyl pierwszy zauważamy, że na pozycjach 15 oraz 16 jest również ta sama liczba i również jest to 1:
$Q_1 = x_{16} = x_{17} = 1$
Tak samo licząc medianę, zauważmy, że tak na pozycji 30, jak i na pozycji 31 jest ta sama liczba i jest to liczba 2, zatem:
$Me = x_{30} = x_{31} = 2$
W przypadku kwartyla trzeciego sytuacja jest odmienna. Zaokrąglając numer kwartyla (45,25) w dół, zauważamy, że na pozycji czterdziestej piątej jest jeszcze liczba 3, ale na kolejnej, czterdziestej szóstej pozycji jest liczba 4. Wobec tego należy użyć średniej ważonej. Jako, że część ułamkowa wynosi 0,25, to wagi wyniosą odpowiednio 0,75 oraz 0,25:
$Q_3 = x_{45} \cdot 0,75 + x_{46} \cdot 0,25 = 3 \cdot 0,75 + 4 \cdot 0,25 = 2,25 + 1 = 3,25$
I tak samo w przypadku dziewiątego decyla. Numer jego pozycji to 54,1. Na pozycji 54. jest jeszcze liczba 4, ale na 55. pozycji jest liczba 5. Wobec tego decyl ten jest średnią ważoną z tych liczb, z wagami równymi odpowiednio 0,9 oraz 0,1:
$d_9 = x_{54} \cdot 0,9 + x_{55} \cdot 0,1 = 4 \cdot 0,9 + 5 \cdot 0,1 = 3,6 + 0,5 = 4,1$
Czy ktoś tak liczy?
Sceptyk może zapytać – skoro na polskich uczelniach, w ramach kursu statystyki, nikt tak nie liczy kwantyli w szeregu szczegółowym, to może jednak nie mam racji? A jeśli mam rację, to może powinienem zgłosić to doniosłe odkrycie? Cóż, na medal Fieldsa jestem już zbyt dorosły – a sposób liczenia wcale nie jest jakiś nieznany, czy przełomowy. Od lat jest bowiem stosowany w arkuszach kalkulacyjnych z najpopularniejszym Excelem na czele. Czytelnik może łatwo sprawdzić, że każdy z zaprezentowanych przykładów w Excelu da identyczny wynik z otrzymanym tutaj – oczywiście dane z przykładu 3 trzeba będzie wprowadzić do Excela, jako szereg szczegółowy, tj. wpisać pięciokrotnie zero, dwanaście razy jedynkę i tak dalej.
Na pytanie: dlaczego na polskich uczelniach uczy się studentów herezji, niestety nie jestem w stanie odpowiedzieć.
